기계학습 문제 대부분은 학습 단계에서 최적의 매개변수를 찾아낸다. 신경망 역시 최적의 매개변수 ( 가중치와 편향 )를 학습시에 찾아야 한다.
여기에서 최적이란 손실 함수가 최솟값이 될 때의 매개변수 값이다.
그러나 일반적인 문제의 손실 함수는 매우 복잡하고, 매개변수 공간이 광대하여 어디가 최솟값이 되는 곳인지를 짐작할 수 없다.
이런 상황에서 기울기를 잘 이용해 함수의 최솟값( 또는 가능한 한 작은 값 ) 을 찾으려는 것이 경사법이다.
여기에서 주의할 점은 각 지점에서 함수의 값을 낮추는 방안을 제시하는 지표가 기울기라는 것이다. 그러나 기울기가 가르키는 곳에 정말 함수의 최솟값이 있는지,
즉 그쪽이 정말로 나아갈 방향인지는 보장할 수 없다. 실제로 복잡한 함수에서는 기울기가 가리키는 방향에 최솟값이 없는 경우가 대부분이다.
NOTE_
함수가 극솟값, 최솟값, 또 안장점(saddle point)이 되는 장소에서는 기울기가 0이다. 극솟값은 국소적인 최솟값, 즉 한정된 범위에서의 최솟값인 점이다.
안장점은 어느 방향에서 보면 극댓값이고 다른 방향에서 보면 극솟값이 되는 점이다. 경사법은 기울기가 0인 장소를 찾지만 그것이 반드시 최솟값이라고는 할 수 없다.
( 극솟값이나 안장점일 가능성이 있다.) 또, 복잡하고 찌그러진 모양의 함수라면 ( 대부분 ) 평평한나 곳으로 파고들면서 고원(plateau)이라 하는, 학습이 진행되지 않는 정체기에 빠질 수 있다.
NOTE_
안장점의 대표적인 예로서 f(x,y) = x^2 - y^2 이다.

기울어진 방향이 꼭 최솟값을 가르키는 것은 아니나, 그 방향으로 가야 함수의 값을 줄일 수 있다. 그래서 최솟값이 되는 장소를 찾는 문제 ( 아니면 가능한 한 작은 값이 되는 장소를 찾는 문제 )
에서는 기울기 정보를 단서로 나아갈 방향을 정해야 한다.
여기서 경사법이 등장한다. 경사법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동한다. 그런 다음 이동한 곳에서도 마찬가지로 기울기를 구하고, 또 그 기울어진 방향으로 나아가기를 반복한다. 이렇게 해서 함수의 값을 점차 줄이는 것이 경사법( gradient method ) 이다. 경사법은 기계학습을 최적화하는데 흔히 쓰는 방법이다. 특히 신경망 학습에는 경사법을 많이 사용한다.
NOTE_
경사법은 최솟값을 찾느냐, 최댓값을 찾느냐에 따라 이름이 다르다. 전자의 경우는 경사 하강법( gradient descent method ) , 경사 상승법 ( gradient ascent method ) 이라고 한다.
다만 손실 함수의 부호를 반전시키면 최솟값을 찾는 문제와 최댓값을 찾는 문제는 같은 것이니 하강인지, 상승인지 본질적인 문제는 중요하지 않다.
일반적으로 경사 하강법을 많이 사용한다.
경사법을 수식으로 나타내보자.


기호 n은 eta, 에타 즉 갱신하는 양을 나타낸다. 이를 신경망 학습에서는 학습률 이라고 한다.
한 번의 학습으로 얼마만큼 학습해야 할지, 즉 매개변수 값을 얼마나 갱신하느냐를 정하는 것이 학습률이다.
위 의 수식은 1회에 해당하는 갱신이고, 이 단계를 계속 반복한다.
즉 위 수식처럼 변수의 값을 갱신하는 단계를 여러 번 반복하면서 서서히 함수의 값을 줄이는 것이다. 또, 여기에서는 변수가 2개인 경우를 보여줬지만, 변수의 수가 늘어나도 같은 식으로 갱신하게 된다.
또한 학습률은 0.01이나, 0.01등 미리 특정 값으로 정해두어야 한다. 일반적으로 이 값이 너무 크거나 작으면 좋은 장소를 찾아갈 수 없다. 신경망 학습에서는 보통 이 학습률
값을 변경하면서 올바르게 학습하고 있는지를 확인하면서 진행해야한다.
경사 하강법을 파이썬으로 간단히 구현해보자.
def gradient_descent(f, init_x, lr = 0.01, step_num=100):
x = init_x
for i in ragne(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
인수 f는 최적화 하려하는 함수, init_x는 초깃값, lr 은 learning rate를 의미하는 학습률, stp_num은 경사법에 따른 반복 횟수를 뜻한다.
함수의 기울기는 numerical_gradient(f, x)로 구하고, 그 기울기에 학습률을 곱한 값으로 갱신하는 처리를 step_num번 반복한다.
이 함수를 사용하면 함수의 극솟값을 구할 수 있고 잘하면 최솟값을 구할 수도 있다. 연습문제를 한번 풀어보자.
연습 문제 ) f(x0,x1) = x0^2 + x1^2의 최솟값을 구하라.
def gradient_descent(f, init_x, lr = 0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
def prac_function(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0,4.0])
print(gradient_descent(prac_function, init_x=init_x, lr=0.1, step_num=100))
[-6.11110793e-10 8.14814391e-10]
초깃값을 (-3,4)로 설정해 시작한다. 최종 결과는 (-6.1e-10, 8.1e-10)으로, 거의 0에 가까운 결과이다. 실제로 진정한 최솟값은 (0,0)이므로 경사법으로 거의 정확한 결과를 도출해낸 것이다.
경사법을 사용한 이 갱신 과정을 그림으로 나타내면 아래와 같다.

적절한 학습률
값이 가장 낮은 장소인 원점에 점차 가까워 지고 있음을 확인할 수 있다.
만약에 학습률을 너무 높게 하거나, 너무 낮게 한다면 어떻게 될까? 한번 확인해보자.
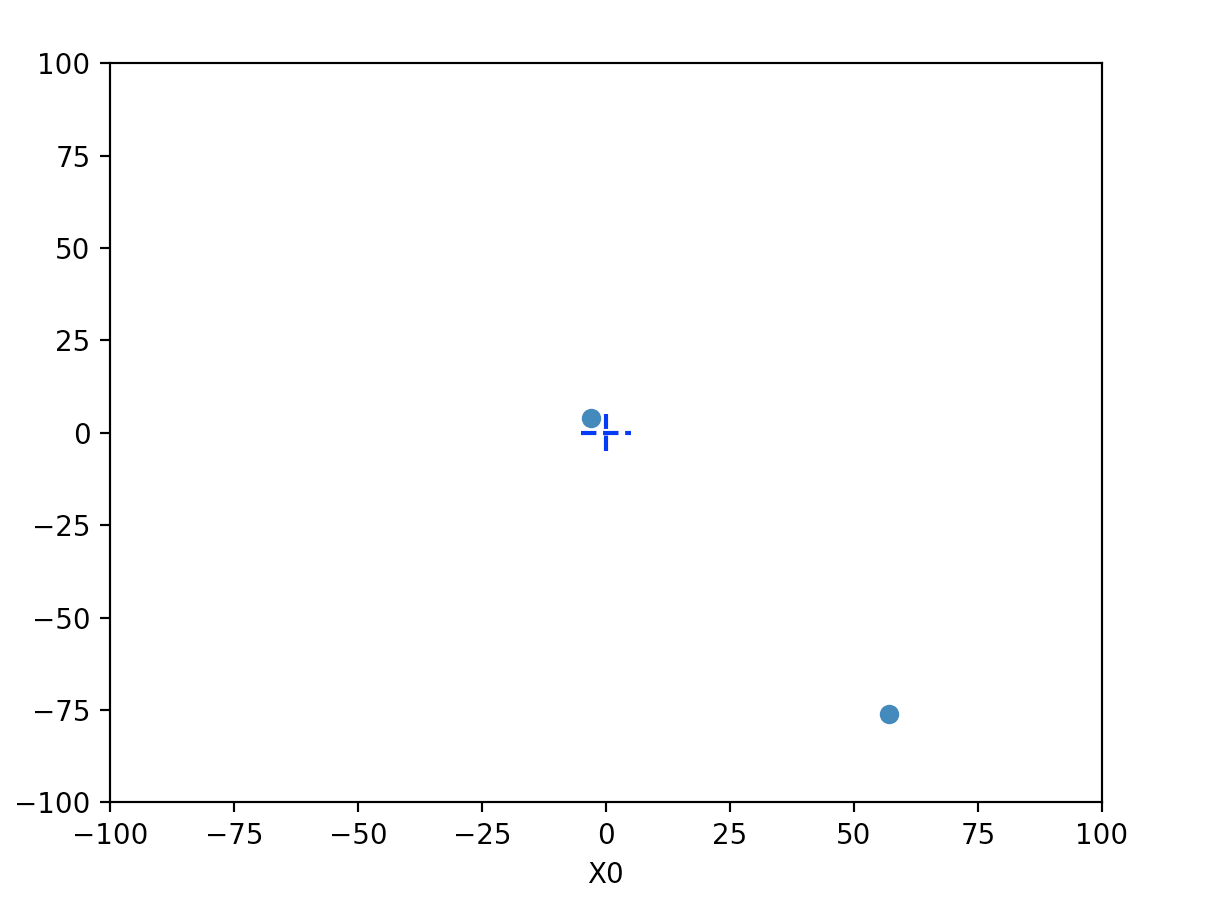
학습률이 10인 경우이다. 너무 큰 값으로 발산해 버린다.

학습률이 1e-10인 경우다. 갱신이 되기도 전에 끝나버린다. 이러한 이유로 학습률의 설정은 매우 중요하다.
NOTE_
학습률 같은 매개변수를 “ 하이퍼 파라미터 “ 라고 한다. ( hyper - parameter, 초매개변수 ) 이는 가중치와 편향 같은 신경망의 매개변수와는 성질이 다른 매개변수이다.
신경망의 가중치 매개변수는 훈련 데이터와 학습 알고리즘에 의해서 ‘자동’으로 획득되는 매개변수인 반면, 학습률 같은 하이퍼파라미터는 사람이 직접 설정해야 하는 매개변수 이다.
일반적으로는 이 하이퍼파라미터 들은 여러 후보 값 중에서 시험을 통해 가장 잘 학습하는 값을 찾는 과정을 거쳐야 한다.