우리가 마라톤 선수라고 가정하고, 10분에 2km씩 뛰었다고 가정해보자. 이때의 속도는 간단히 거리 = 속력 * 시간 이므로,
2 / 10 = 0.2[km/분]이라고 계산 한다. 즉 1분에 0.2km만큼의 속도 (변화)로 뛰었다고 해석한다.
이 마라톤 에서는 ‘달린 거리’가 ‘시간’에 대해서 얼마나 변화했는가를 계산 했다.
다만 여기에서 10분에 2km를 뛰었다는 것은, 정확하게 10분 동안의 ‘평균 속도’를 계산한 것이다.
미분은 “ 특정 순간의 변화량 “ 을 의미한다. 그래서 10분이라는 시간을 가능한 한 줄여 ( 직전 1분에 달린 거리, 직전 1초에 달린 거리, 직전 0.1초에 달린 거리, …. lim를 생각해보자.)
한 순간의 변화량 ( 어느 순간의 속도 ) 를 얻는 것이다.
이처럼 미분은 한순간의 변화량을 표시한 것이다. 수식으로는 아래와 같다.
$\frac{df\left(x\right)}{dx}=\lim _{\combi{h}\to \combi{0}}^{ }\combi{\frac{f\left(x+h\right)\ -\ f\left(x\right)}{h}}$df(x)dx=limh→0f(x+h) − f(x)h
좌변은 f(x)의 x에 대한 미분( x에 대한 f(x)의 변화량 )을 나타내는 기호. 결국, x의 작은 변화가 f(x)를 얼마나 변화시키냐를 의미 한다.
( 바로 전 게시물에서 한 내용이 생각나지 않나요? )
이때 시간의 작은 변화, 즉 시간을 뜻하는 h를 한없이 0에 가깝데 한다는 의미로 lim로 나타낸다.
이 미분을 파이썬으로 구현해보자.
이때 곧이 곧대로 구현하려면 h에 작은 값을 대입해 다음과 같이 계산할 수 있다.
def numerical_diff(f, x):
h = 10e-50
return ( f(x+h) - f(x) ) / h
함수의 이름은 수치 미분 ( numerical_differentitation ) 에서 따왔다.
이 함수는 “ 함수 f와 “ “함수 f에 넘길 인수 x ‘ 라는 두 인수를 받는다. 하지만 이 함수는 개선해야할 문제점이 2개가 있다.
앞의 구현에서는 h에 가급적 작은 값을 대입하고 싶었기에, 10e-50을 이용했지만, 이 값은 0.00…..1 형태에서 0이 50개라는 의미이다.
그러나 이 방식은 반올림 오차 ( rounding error ) 를 일으킨다. 반올림 오차는 작은 값 ( 가령 소수점 8자리 이하 ) 가 생략되어 최종 계산 결과에 오차가 생기게 한다.
이것이 첫번째 개선 방법이다.
1e-50은 너무 작은 숫자가 되어 0.0이 되어 올바르게 나타낼수 없다. 리미트를 이용해 0으로 보내는것이지, 0은 아니기 때문이다.
이 미세한 값을 h로 10^-4를 사용해본다. 이 값은 좋은 결과를 나타낸다고 알려져 있다.
두 번째 개선은 함수 f의 차분과 관련된 것이다. 앞의 구현에서는 x + h 와 x 사이의 함수 f의 차분을 계산하고 있지만, 애당초 이 계산은 잘못되었다.
진정한 미분은 x 위치의 함수의 기울기 ( 이를 접선이라 함 ) 에 해당하지만, 이번 구현에서의 미분은 ( x + h ) 와 x 사이의 기울기에 해당되기 때문이다.
그래서 미분과 이번 구현의 값은 엄밀히 일치하지 않는다.
이 차이는 무한히 h를 0으로 좁히지 못하기 때문에 발생하는 것이다.

연산결과에는 알맞지 않지만 이해를 편하게 하기 위해 그래프를 가져왔다.
미분을 하려고 하는 f(x) = sinx 이다.
f’(x) = x 라고 가정할때,
우리는 진정한 미분을 하지 못해 f’(x) = 2x가 도출되게 된것이다.
진정한 미분과 수치 미분의 값은 다르다.
위의 그림과 같이, 수치 미분에는 오차가 포함된다. 이 오차를 줄이기 위해 ( x + h ) 와 ( x - h ) 일 때의 함수의 차분을 계산하는 방법을 사용하기도 한다.
이 차분은 x를 중심으로 그 전후의 차분을 계산한다는 의미에서 중심 차분, 혹은 중앙 차분이라고 한다.
한편 x + h 와 x의 차분은 전방 차분이라고 한다.
개선점을 적용해 파이썬으로 구현해 보자.
def numerical_diff(f, x):
h = 1e-4
return ( f(x+h) - f(x-h) ) / (2*h)
NOTE_
여기에서 하는 것처럼 아주 작은 차분으로 미분하는 것을 “ 수치 미분 “ 이라고 한다. 한편, 수식을 전개해 미분하는 것은 해석적 이라는 말을 이용한다.
해석적 미분은 오차를 포함하지 않는 “ 진정한 미분 “ 값을. 구해준다.
간단히 말해 해석적 미분은 우리가 수학 시간에 배운 바로 그 미분이고, 수치 미분은 이를 근사치로 계산하는 방법이다.
수치해석학은 “ 해석학 문제에서 수치적인 근삿값을 구하는 알고리즘을 연구하는 학문이다"
앞 의 수치 미분을 사용하여 간단한 함수를 미분해보자. 아래의 식은 간단한 2차 함수이다.
f(x) = 0.01x^2 + 0.1x
이 식을 파이썬으로 구현하면 아래와 같다.
def function(x):
return 0.01 * x ** 2 + 0.1 * x
이 수식을 파이썬의 matplotlib.pylab 을 사용하여 그래프로 나타내보자.
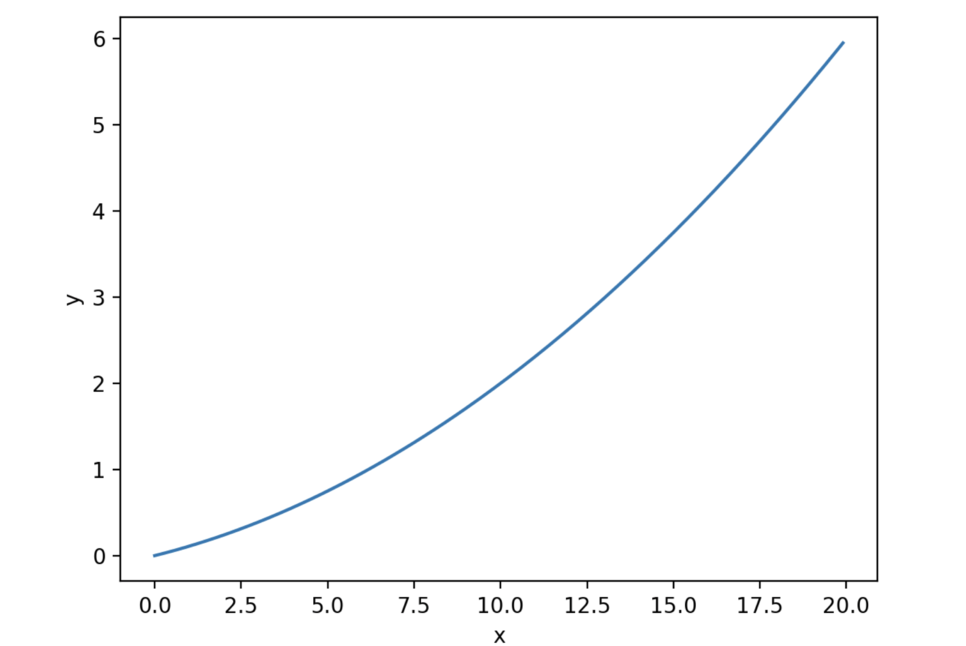
이 때의 x = 5, x = 10 일때의 함수를 미분해보자.
소스코드는 아래와 같다.
import numpy as np
from matplotlib import pylab as plt
def function(x):
return 0.01 * x ** 2 + 0.1 * x
def numerical_diff(f, x):
h = 1e-4
return ( f(x+h) - f(x-h)) / (2*h)
x = np.arange(0.0, 20.0, 0.1) # 0 에서 20까지 0.1 간격의 배열인 x를 생성한다.
y = function(x) # y=f(x)
plt.xlabel("x") # 그래프 상의 x축 이름 설정
plt.ylabel("y") # 그래프 상의 y축 이름 설정
plt.plot(x,y)
plt.show() # 그래프 보여주기.
print(numerical_diff(function, 5))
print(numerical_diff(function, 10))
0.1999999999990898
0.2999999999986347
실제로 수학시간에 배운 미분법을 적용하면, 차례대로 f’(5) = 0.2, f’(1) = 0.3 이다.
앞의 수치 미분과 결과를 비교하면 매우 오차가 작다.
이제 앞에서 구한 수치 미분 값을 기울기로 하는 직선을 그려보자.

'머신러닝, 딥러닝' 카테고리의 다른 글
| 기울기 (0) | 2020.01.20 |
|---|---|
| 편미분 (0) | 2020.01.20 |
| 왜 손실함수를 사용하는가? (0) | 2020.01.20 |
| 미니 배치 학습 (0) | 2020.01.20 |
| 교차 엔트로피 오차 ( Cross Entropy Error, CEE ) (0) | 2020.01.20 |



